Explorando los Enigmas de las Matemáticas: Cómo los Problemas del Milenio Podrían Revolucionar la Salud por Carlos Salinas Diciembre 2023

P versus NP

Si se resuelve este problema, podríamos desarrollar algoritmos capaces de procesar y analizar grandes conjuntos de datos médicos de manera más eficiente. Esto significa diagnósticos más rápidos y precisos, tratamientos personalizados y una mejor gestión de los recursos sanitarios.

El problema P vs NP es uno de los problemas abiertos más importantes en informática teórica y matemáticas. Se relaciona con la clasificación y la dificultad de resolver ciertos tipos de problemas. Aquí está una explicación breve:

1. Clase P (Tiempo Polinómico): P es la clase de problemas que pueden ser resueltos rápidamente por una computadora. "Rápidamente" aquí significa en tiempo polinómico en relación al tamaño de la entrada; es decir, el tiempo que se tarda en resolver el problema crece a lo sumo como un polinomio en función del tamaño de la entrada.

2. Clase NP (Tiempo No determinístico Polinómico): NP es la clase de problemas para los cuales, dada una solución, podemos verificar si esa solución es correcta en tiempo polinómico. Esto no significa necesariamente que podamos encontrar esa solución rápidamente; solo que si alguien nos da una solución, podemos verificarla eficientemente.

3. La Pregunta P vs NP: La pregunta central es si toda clase de problemas que están en NP también están en P. En otras palabras, ¿es posible resolver todos los problemas para los cuales podemos verificar soluciones rápidamente también rápidamente? Si P = NP, significaría que para todos los problemas que podemos verificar una solución rápidamente, también podemos encontrar esa solución rápidamente.

Esta imagen simboliza el desafío de resolver problemas complejos en salud, como el análisis de datos médicos y la interpretación del ADN.

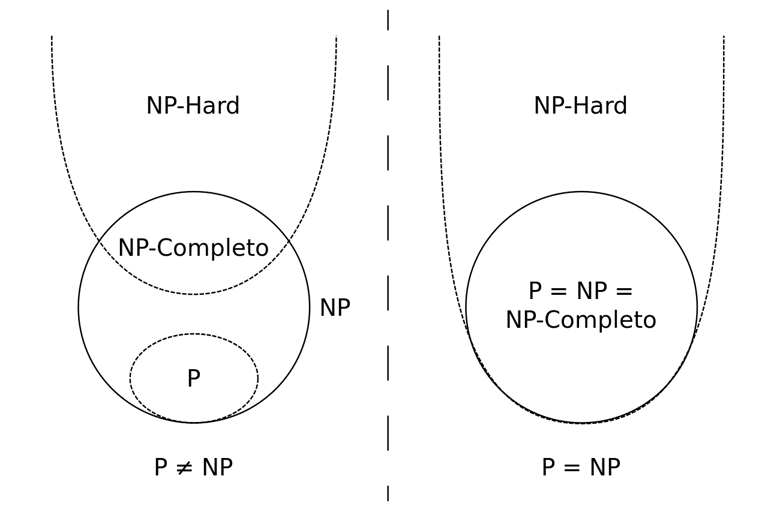
A la izquierda, se muestra que P es diferente de NP, con los problemas NP-Completos y NP-Duros no necesariamente solubles en tiempo polinómico.

A la derecha, se muestra que P es igual a NP, lo que implicaría que todos los problemas verificables rápidamente también son solubles rápidamente, incluyendo los NP-Completos y NP-Duros.

Conjetura de Hodge

Su solución podría influir en la manera en que entendemos las formas geométricas y estructuras en biología, desde la forma de las proteínas hasta la organización de las células en tejidos, abriendo nuevas puertas en la bioinformática y el diseño de fármacos.

En pocas palabras, la Conjetura de Hodge es un problema no resuelto en el campo de la geometría algebraica, que trata sobre las formas en que ciertas clases de formas geométricas (llamadas ciclos algebraicos) se relacionan con la topología de un espacio complejo.
La Conjetura de Hodge tiene implicaciones profundas para la comprensión de la geometría y la topología de las variedades algebraicas y, si se resuelve, podría proporcionar una comprensión más profunda de la estructura y las propiedades de los espacios .

La conjetura de Hodge se relaciona la topología algebraica de una variedad algebraica compleja no singular y las subvariedades de esa variedad. En concreto, la conjetura dice que ciertos grupos de cohomología de De Rham son algebraicos, esto es, son sumas de dualidades de Poincaré de clases homólogas de subvariedades.

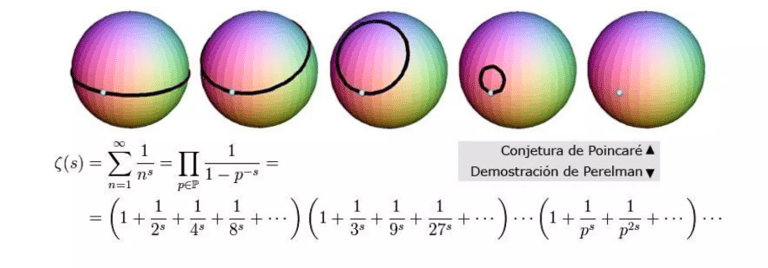
La siguiente ecuación matemática que expresa la descomposición de Hodge en cohomología. La ecuación es:

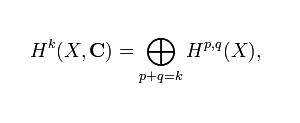
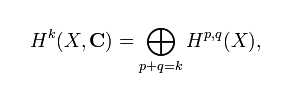
El k-ésimo grupo de cohomología H^k de una variedad compleja X con coeficientes en los números complejos C puede ser descompuesto en una suma directa de espacios H^(p,q)(X), que son grupos de cohomología de Hodge. Estos grupos de cohomología de Hodge corresponden a las formas diferenciales de tipo (p,q) en la variedad X, donde la suma de p y q es igual a k.

Hipótesis de Riemann

Resolverla podría mejorar nuestra comprensión de la estadística y la probabilidad, fundamentales en la investigación epidemiológica y en la toma de decisiones basada en evidencia en salud pública.

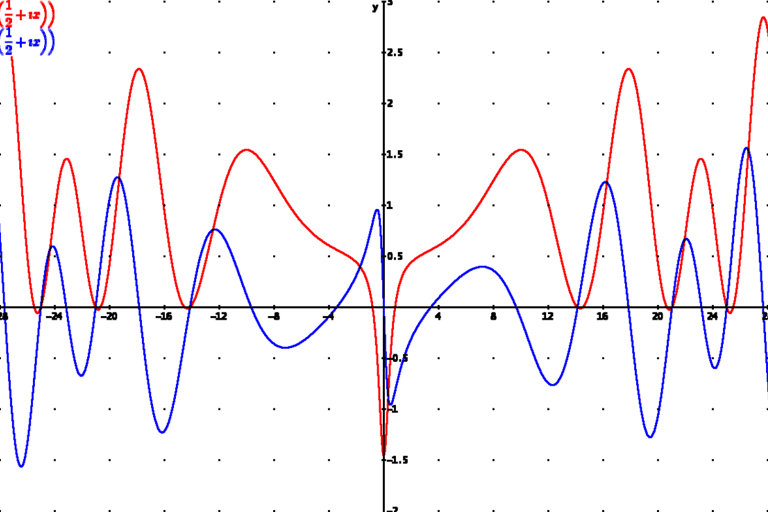
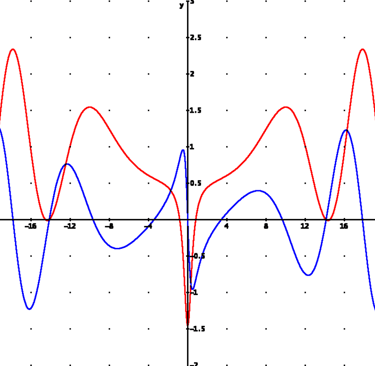
Representación gráfica de la función zeta de Riemann en el plano complejo, mostrando la parte real e imaginaria de la función zeta para valores específicos de s. La línea azul representa la parte real de ζ(s), y la línea roja representa la parte imaginaria. La Hipótesis de Riemann se refiere a la localización de los ceros no triviales de esta función, que se cree están en la línea crítica, donde la parte real de s es 1/2.

Existencia y Brecha de Masa de Yang-Mills

Esta teoría está en la base de nuestra comprensión de las fuerzas fundamentales de la física, lo que podría llevar a avances en tecnologías como la imagen por resonancia magnética (IRM) y otros métodos de diagnóstico por imágenes podría decirse que tendríamos imagenes de resonancia cuántica.

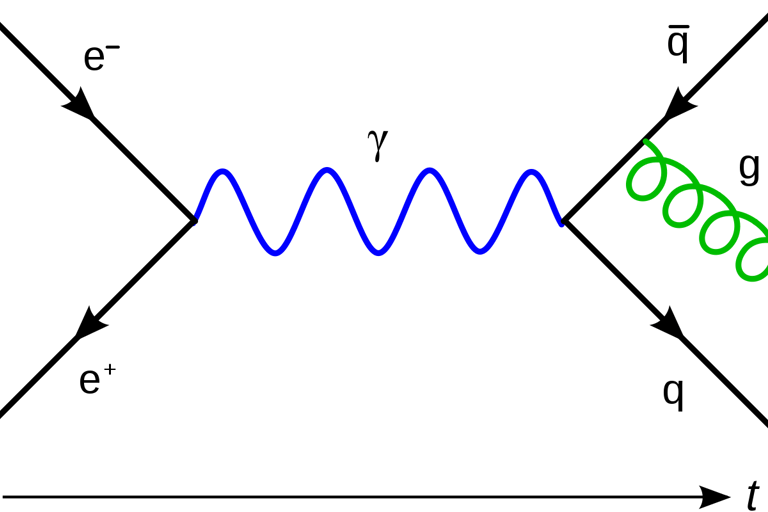
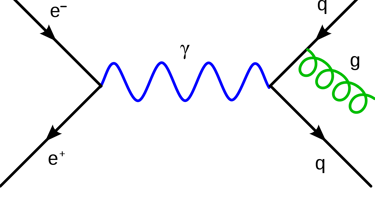
Un campo de Yang-Mills es un campo físico que describe la interacción entre las partículas fundamentales. Se utiliza en la teoría cuántica de campos, que es una teoría física que describe la naturaleza a nivel subatómico.

El campo de Yang-Mills tiene una propiedad llamada invariancia de gauge local. Esta propiedad significa que las ecuaciones que describen el campo no cambian si se aplican una transformación de gauge local, que es una transformación que cambia la forma en que se mide el campo.

Los campos de Yang-Mills son importantes porque son el fundamento de las tres fuerzas fundamentales de la naturaleza: la fuerza electromagnética, la fuerza débil y la fuerza fuerte.

Existencia y Suavidad de Navier-Stokes

Comprender estas ecuaciones puede tener aplicaciones directas en la modelización del flujo sanguíneo y la dinámica de fluidos en el cuerpo humano, crucial para el tratamiento de enfermedades cardiovasculares y la cirugía vascular.

No incluí la conjetura de Poincaré porque ya se ha resuelto, sin embargo siempre hay espacio para la optimización.

Referencia:

Carlson, J., Jaffe, A., & Wiles, A. (Eds.). (2006). The millennium prize problems: A history of prizes in mathematics. Clay Mathematics Institute & American Mathematical Society.